Computing improper integrals with Cauchy's residue theorem
mathematicsSo, Gianni Sarcone, an artist, author, and a designer, mostly known for his optic illusions, brought to my attention an integral that combines \(\pi\) and \(e\) constants in the following elegant manner:
\[\int_{-\infty}^{\infty} \frac{\cos{x}}{(x^2+1)^2}\mathrm{d}x = \frac{\pi}{e}\]Let’s take a look at the function that we will be integrating:
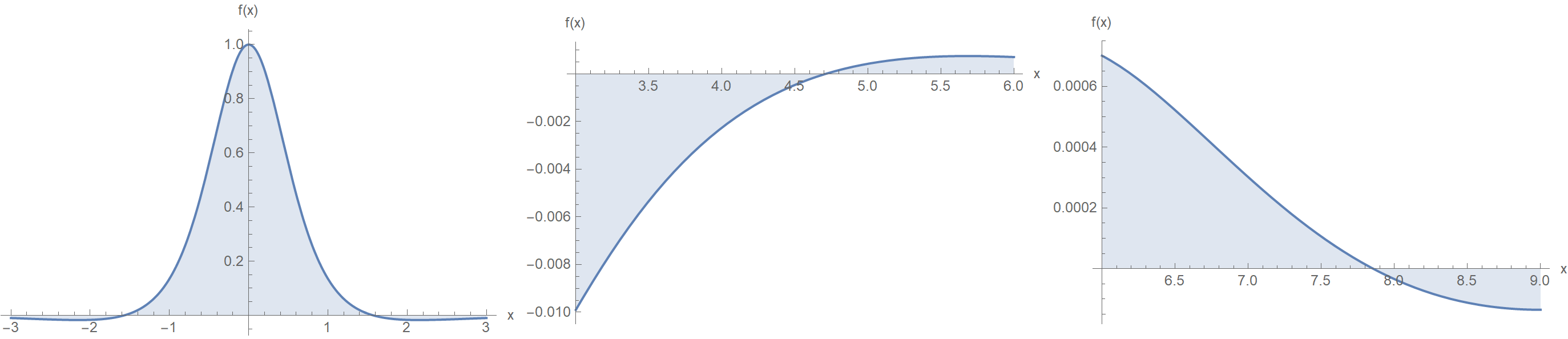
Such integrals, where the endpoints go to infinity, are called improper. Perhaps this one can be calculated via some substitution or Feynman’s differentiation technique under the integral sign. However, I decided to use the nuclear bomb of the integration arsenal, the Cauchy residue theorem of complex analysis.
\[\oint_\gamma f(z)\, \mathrm{d}z = 2\pi i \sum_{k=1}^n \operatorname{I}(\gamma, a_k) \operatorname{Res}( f, a_k )\]Where \(I(\gamma, a_k)\) is the winding number, which for simple curves is equal to one, and \(\operatorname{Res}(f,a_k)\) is the k-th residue of the function \(f\). The \(a_k\) points must be finite, and \(f\) be holomorphic on a simply connected open subset of the complex plane. Finally, the curve \(\gamma\) is a closed curve that does not meet any of the \(a_k\) points.
We start by considering the function:
\[f(z)=\frac{\cos{z}}{(z^2+1)^2}\]Now here comes the tricky part. If we try to do a direct contour integral, it won’t work because the cosine in the complex plane blows up for large imaginary numbers in both half-planes.
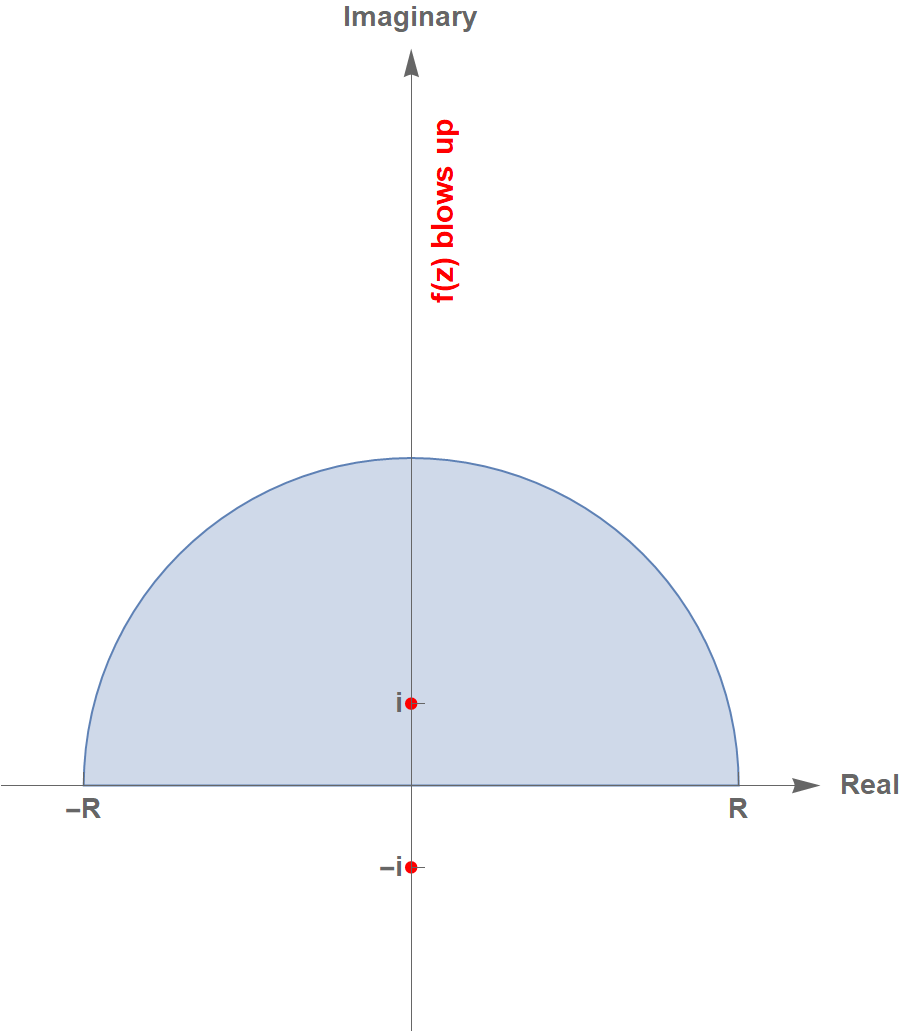
So we will instead calculate the contour integral of:
\[\oint_\gamma \frac{e^{i z}}{(z^2+1)^2} \mathrm{d}z\]Check the following 3D plots of \(\operatorname{Abs}(f)\) colored by \(\operatorname{Arg}(f)\) over a region of the complex plane. Notice the existence of poles, but more importantly, notice how \(\cos(z)\) blows up on both half-planes, whereas the one with the exponential in the numerator blows up only on the negative half-plane.

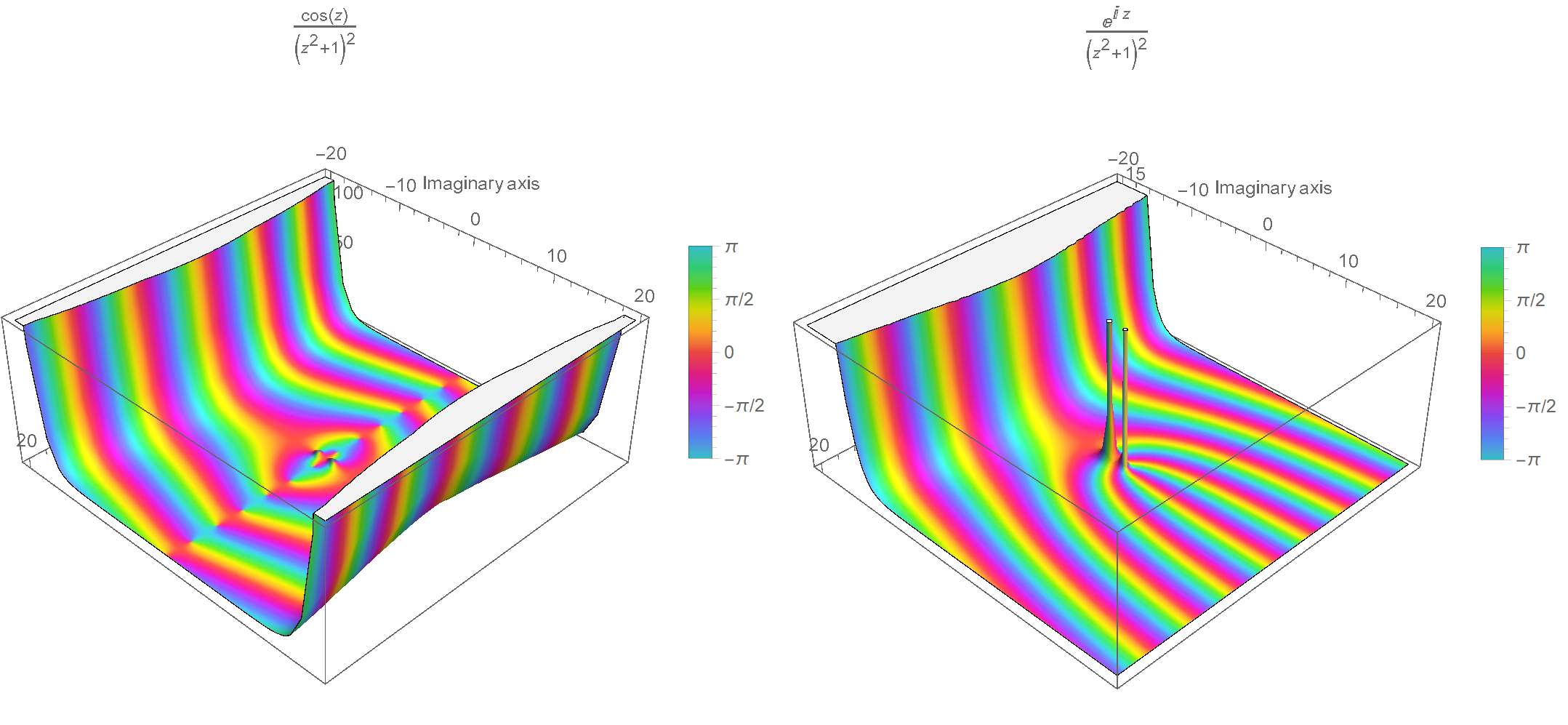
So, we break the contour integral into two parts: \(\begin{align*} \oint_\gamma \frac{e^{i z}}{(z^2+1)^2} \mathrm{d}z &= \int_{-R}^R \frac{e^{i z}}{(z^2+1)^2} \mathrm{d}z + \int_{\gamma_R} \frac{e^{i z}}{(z^2+1)^2} \mathrm{d}z = 2\pi i \sum_{k=1}^n \operatorname{Res}( f, a_k ) \Rightarrow\\ \int_{-R}^R \frac{e^{i z}}{(z^2+1)^2} \mathrm{d}z &= 2\pi i \sum_{k=1}^n \operatorname{Res}( f, a_k ) - \int_{\gamma_R} \frac{e^{i z}}{(z^2+1)^2} \mathrm{d}z \end{align*}\)
We then apply Cauchy’s residue theorem and take the limit as \(R\to\infty\):
\[\text{P.V.} \int_{-\infty}^{\infty} \frac{e^{i x}}{(x^2+1)^2} \mathrm{d}x = \lim_{R\to\infty}\left( 2\pi i \sum_{j=1}^n \operatorname{Res}(f, a_k)\right) - \underbrace{\lim_{R\to\infty} \int_{\gamma_R} \frac{e^{i z}}{(z^2+1)^2} \mathrm{d}z}_{\substack{\text{This is zero.}\\ \text{If cos was at the numerator,}\\ \text{it would blow up.}}}\]The singular points in the complex plane are when the denominator is zero:
\[(z^2+1)^2 =0 \Leftrightarrow \left[(z+i)(z-i)\right]^2=0 \Leftrightarrow (z+i)^2 (z-i)^2 = 0 \Leftrightarrow \left\{z=i,z=-i\right\}\]Therefore we have a pole of second order at \(z = i\). Its residue is:
\[\begin{align*} \operatorname{Res}(f, z=i) &= \frac{1}{(2-1)!}\lim_{z\to i}\frac{\partial }{\partial z} \left[ (z-i)^2\frac{\exp (i z)}{(z+i)^2 (z-i)^2}\right]\\ &= \lim_{z\to i}\frac{\partial }{\partial z} \left[ \frac{\exp (i z)}{(z+i)^2 }\right]\\ &= \lim_{z\to i}\frac{i \exp(i z) (z+i)^2 - 2\exp(iz)(z+i)}{(z+i)^4}\\ &= \frac{i e^{-1}4i^2 - 2e^{-1}2i}{(2i)^4} = \frac{-4i-4i}{16e} = -\frac{i}{2e} \end{align*}\]Finally:
\[\text{P.V.} \int_{-\infty}^{\infty} \frac{e^{i x}}{(x^2+1)^2} \mathrm{d}x = \lim_{R\to\infty}\left[ 2\pi i \left(-\frac{i}{2e}\right)\right] = \frac{\pi}{e}\]How to taint the beauty
Suppose that we are only interested in an approximate value of the integral. We can then make two assumptions. First, we will integrate the function from \([-\pi/2, \pi/2]\), because that’s the part of the function that contributes most to the integral’s value (see also the first figure). The second assumption comes from the fact that we will approximate the cosine with its Taylor series: \(\cos x = 1 - x^2/2 + \mathcal{O}(x)^3\):
\[\begin{align*} I=\int_{-\infty}^{\infty} \frac{\cos x}{(x^2+1)^2}\mathrm{d}x &\simeq \int_{-\pi/2}^{\pi/2} \frac{\cos x}{(x^2+1)^2}\mathrm{d}x =2\int_{0}^{\pi/2} \frac{\cos x}{(x^2+1)^2}\mathrm{d}x\\ &\simeq 2\int_{0}^{\pi/2} \frac{1-\frac{x^2}{2}}{(x^2+1)^2}\mathrm{d}x =\int_{0}^{\pi/2} \frac{2-x^2}{(x^2+1)^2}\mathrm{d}x \end{align*}\]We make the substitution:
\[x = \tan\theta \Rightarrow \mathrm{d}x=1/\cos^2\theta \mathrm{d}\theta\]And the new interval is \([\tan^{-1}(0),\tan^{-1}(\pi/2)] = [0,\tan^{-1}(\pi/2)]\). Then, we write:
\[\begin{align*} I &= \int_{0}^{\tan^{-1}(\pi/2)} \frac{2-\tan^2\theta}{\left(\tan^2\theta + 1\right)^2} \frac{1}{\cos^2\theta}\mathrm{d}\theta = \int_{0}^{\tan^{-1}(\pi/2)} \frac{2-\tan^2\theta}{1/\cos^4\theta}\frac{1}{\cos^2\theta} \mathrm{d}\theta\\ &=\int_{0}^{\tan^{-1}(\pi/2)} \left(2\cos^2\theta-\sin^2\theta \right) \mathrm{d}\theta = \left[\frac{\theta}{2} + \frac{3}{4}\sin(2\theta)\right]_0^{\tan^{-1}(\pi/2)} \simeq 1.181 \end{align*}\]So we got:
\[\int_{-\infty}^{\infty} \frac{\cos x}{(x^2+1)^2}\mathrm{d}x \simeq 1.181\]Whereas the precise value is:
\[\int_{-\infty}^{\infty} \frac{\cos x}{(x^2+1)^2}\mathrm{d}x = \pi/e \simeq 1.156\]The relative error is \(\sim 2.16\%\). That’s not bad at all, given how many things we left out during our assumptions! Ugly? Perhaps. Neat? Definitely!