What does it really mean for a machine to learn mathematics?
machine learning mathematics neural networksContents
Introduction
This post was triggered by a paper posted here, titled “Deep learning from symbolic mathematics”. The authors trained a sequence-to-sequence neural network that was able to perform symbolic integration and solve differential equations. Remarkably, they achieved results that outperform commercial Computer Algebra Systems (CAS) such as Matlab and Mathematica. It’s interesting to see how they built their training set.
Training sets
Integration
The training set for integration was generated by assuming random functions (with an upper length limit) and calculating their derivatives with a CAS. Then, the derivatives became the input targets, and the original functions the output. For instance, suppose that we start with the function:
\[f(x) = \ln(\ln(x)) \Rightarrow f'(x) = \frac{1}{\ln(x)} \cdot (\ln(x))' = \frac{1}{x \ln(x)}\]Then, in our training set we consider \(\frac{1}{x \ln(x)}\) to be the input, i.e. the function that we want to integrate, and \(\ln(\ln(x))\) becomes the desired output of our model.
\[\int \frac{1}{x \ln(x)} \mathrm{d}x = \ln(\ln(x)) + C\]Solving first-order differential equations
The training set for solving first-order differential equations is generated in a similar way, i.e. with a “reverse logic”. Let’s start with a random function of two variables \(F(x,y) = c\), where \(c\) is some constant. Then, if \(F\) is chosen such that it is “solvable for \(y\)”, meaning that we can write \(y = f(x, c) = f_c(x)\), the function \(F\) can be expressed as \(F(x, f_c(x)) = c\). Differentiating with respect to \(x\), we get:
\[\frac{\partial F(x, f_c(x))}{\partial x} + \frac{\partial F(x,f_c(x))}{\partial f_c(x)} \frac{\partial f_c(x)}{\partial x} = 0\]Recall that when we want to calculate the total derivative of a function \(y = f(t, u_1, u_2, \ldots)\), where the intermediate variables \(u_k\) are functions of the form \(u_k = u_k(t, u_1, u_2, \ldots)\), then \(\frac{\partial y}{\partial t} = \frac{\partial f}{\partial t} + \frac{\partial f}{\partial u_1}\frac{\partial u_1}{\partial t} + \ldots\), since \(y\)’s value are affected directly by \(t\) but also indirectly via the intermediate variables \(u_k\) that are functions of \(t\) as well. If we let \(y = f_c(x)\), then:
\[\frac{\partial F(x, y)}{\partial x} + \frac{\partial F(x, y)}{\partial y} \frac{\partial y}{\partial x} = 0\]Therefore, first, we find the solution \(y = f_c(x)\) of an equation that doesn’t yet exist, and then we construct the equation, i.e.
\[\frac{\partial F(x, y)}{\partial x} + \frac{\partial F(x, y)}{\partial y} y' = 0\]It feels like cheating, huh? Here is a really simple example where we consider \(F(x,y) = x \ln{y}\):
\[\underbrace{x \ln{y}}_{F(x,y)} = c \Rightarrow \ln{y} = c/x \Rightarrow y = e^{c/x}\]Then by differentiating with respect to \(x\), we get:
\[\ln{y} + \frac{x}{y}y' = 0 \Rightarrow x y' + y\ln{y} = 0\]You might want to verify that \(y = e^{c/x}\) is a solution of \(x y' + y\ln{y} = 0\). So \(y = e^{c/x}\) becomes the target of the neural network and \(x y' + y\ln{y} = 0\) the input, i.e. the differential equation that we’d like to solve.
Representing mathematical expressions as sequences
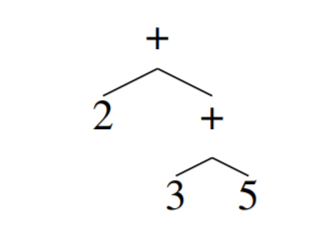
Mathematical expressions are modeled as trees with operators as internal nodes and numbers, constants or variables, as leaves. The authors transformed trees into sequences suitable for natural language processing models by enumerating nodes in prefix order. For example the expression \(2 + 3 + 5\) is represented by the sequence “+ 2 + 3 5”.
From here, it’s standard theory of sequence to sequence models.
To sum up, we generate pairs of derivatives - antiderivatives and pairs of differential equations - solutions, then we convert these expressions to trees and then to sequences. We train a neural network to accept such sequences and output other sequences, where hopefully, the output, when interpreted as a math expression, is the correct solution to the input.
Thoughts
Is pattern matching the same as “mathematical understanding”?
Probably not, but that’s ok.
Suppose I am with someone that doesn’t know anything about mathematics, and I provide him with a list of matching rules like:
\[\begin{align*} x^2 &\longrightarrow 2 x^1\\ x^3 &\longrightarrow 3 x^2\\ x^4 &\longrightarrow 4 x^3\\ x^5 &\longrightarrow 5 x^4\\ x^6 &\longrightarrow 6 x^5\\ x^7 &\longrightarrow 7 x^5\\ \ldots \end{align*}\]After looking at these symbols, he might figure that the expression \(x^{\text{whatever}}\) is mapped to \(\text{whatever} \cdot x ^{\text{whatever} - 1}\). When asked to derive \(x^{100}\), he writes \(100 x^{99}\). Does this mean that he knows how to differentiate the expression \(x^n\)? Even if we accept that he really knows, does he really understand? Since the theory of continuity, limits, and derivatives escapes him, he will most likely miss all the intuition behind derivation, such as:
- The derivative as the rate of change.
- The derivative as the slope of the tangent.
- The derivative \(n x^{n-1}\) as the best linear approximation of \(x^n\).
- That since \(x^n\) is differentiable at some point \(\alpha\), then \(x^n\) is also continuous at \(x = \alpha\).
We (the humans) don’t learn to differentiate by looking at thousand of derivative - antiderivative pairs. Instead, we learn from a bottom-up approach by studying the underlying theory. Therefore, is it fair to expect an AI model to pick up the intuition behind differentiation merely by being presented with tons of matching rules? When a human couldn’t possibly pick it up either? In any case, it would help if we could look at the insides of a neural network and see how the mapping is represented.
The utilitarian point of view
The utilitarian approach states that as long as the neural network model outputs correct answers, it doesn’t matter whether this constitutes a deeper understanding of maths or not. Even if it is merely a pattern matching ability acquired and perfected through the presentation of hundreds of thousands of examples, who cares?
In this context, we may see CAS integrating (no pun intended :P) neural network models in their solvers in a few years. In the most conservative implementations, the solver would first try to apply all the hard-coded rules and heuristics to solve the problem. If it failed to do so, then the output of a neural network model could be checked for correctness. In a more aggressive setup, the neural network’s prediction would be given priority. Remember that for integration and differential equation solving, verification is straightforward and very fast compared to actually solving the problem from scratch.