Bayes theorem and likelihood ratios for diagnostic tests

I was taking a look at a course in medical research methodology and I stumbled upon the following problem.

Suppose that the probability of a patient having a certain disease is \(10\%\) in the general population. Suppose also that the likelihood ratio (LR) for positive result for some diagnostic test is \(1.8\). What is then the probability of a patient having the disease if he tested positive for this diagnostic test?

The likelikood ratio in the context of a diagnostic test is defined in the following way. For positive tests:

\[LR^+ = \frac{\text{specificity}}{1-\text{sensitivity}} = \frac{\text{TPrate}}{\text{FPrate}} = \frac{P(T^+|D^+)}{P(T^+|D^-)}\]

And for negative tests:

\[LR^- = \frac{1-\text{sensitivity}}{\text{specificity}} = \frac{\text{FNrate}}{\text{TNrate}} = \frac{P(T^-|D^+)}{P(T^-|D^-)}\]

So, an \(LR^+ > 1\) indicates that the test result is associated with the disease. If \(LR^+ = 1\) the post-test probability is the same as the pre-test probability. The likelihood ratio, in the latter case, does not add any extra information on what we already know regarding our patient’s risk.

Let’s see how likelihood ratio \(LR^+\) affects our prior credence on whether our patient has indeed the disease. When we want to calculate the probability of an event based on prior knowledge of conditions that might be related to the event, we invoke the Bayes theorem. Let’s calculate the probability that the patient has the disease (\(D^+\)) given that the diagnostic test is positive (\(T^+\)).

Then:

\[\begin{align*} P(D^+|T^+) &= \frac{P(T^+|D^+) P(D^+)}{P(T^+)} \\ &=\frac{P(T^+|D^+) P(D^+)}{P(T^+|D^+)P(D^+) + P(T^+|D^-)P(D^-)} =\\ &= \frac{P(D^+)}{P(D^+) + \frac{P(T^+|D^-)}{P(T^+|D^+)}P(D^-)}\\ &= \frac{P(D^+)}{P(D^+) + \frac{P(D^-)}{LR^+}}\\ &= \frac{0.1}{0.1 + \frac{0.9}{1.8}} = 1/6 \end{align*}\]

So, we started with a prior probability of \(10\%\) and when we took into account the likelihood ratio for this particular diagnostic test that our patient tested positive for, we updated the probability into \(\sim 17\%\).

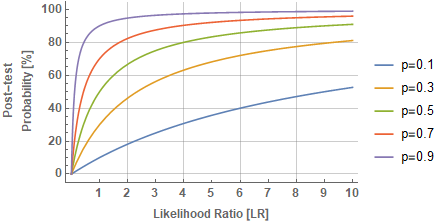
Here is a plot of the post-test probability (%) as a function of LR for various values of prior-test probability:

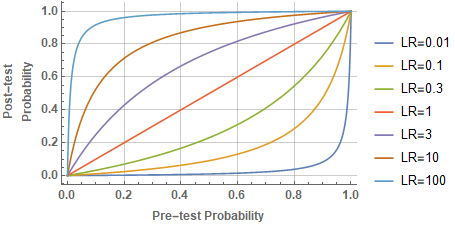
And here is another plot of the post-test probability as a function of prior-test probability for various values of LR. Notice how for an LR equal to 1, the line is \(y=x\), since the probability does not change.

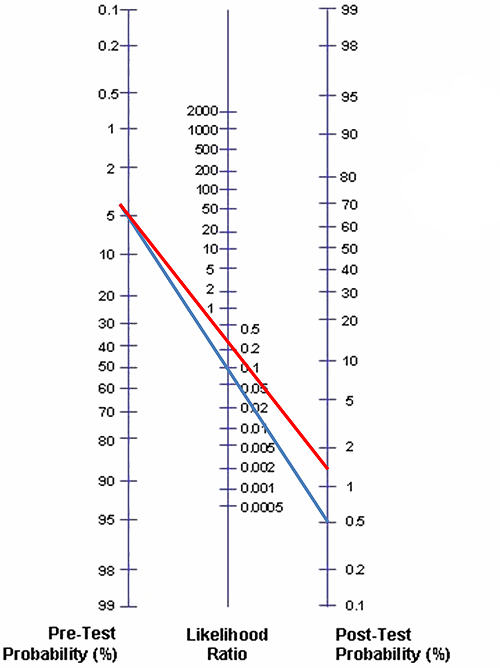
The Fagan nomogram is a graphical tool for estimating how much the result of a diagnostic test changes the probability that a patient has the disease in question. See also “Fagan TJ. Letter: Nomogram for Bayes theorem. N Engl J Med. 1975;293(5):257”. To use the nomogram, you need to have an estimate of the probability of the disease prior to testing. This estimate can be based on the prevalence of the disease modified accordingly by considering other risk factors your patient has. You also need to know the likelihood ratio for the diagnostic test (obviously). So, if you know these two numbers and connect them with a line on the nomogram, the point at which this line intersects with post-test probability is the updated probability of your patient having the disease after having been tested positive for this diagnostic test.