Longest substring with non-repeating characters
algorithms Leetcode programming PythonI have been doing some interviews for job positions like data scientist, machine learning engineer, and software developer during the past months. To prepare for the coding part of these interviews and brush up on my algorithmic thinking and programming skills, I decided to do some ad-hoc practicing. There are lots of websites with coding challenges of varying difficulty. Some examples include Leetcode, HackerRank, Topcoder, and others. Although I kind of dislike the contrived nature of these quizzes, I joined Leetcode nonetheless. Anyway, I picked a problem under the “medium” difficulty category that I’ll blog about today. The problem is about finding the longest substring with non-repeating characters in a string.
Problem formulation
Given a string s, find the length of the longest substring without repeating characters.
Example 1: Input: s = “abcabcbb” Output: 3 Explanation: The answer is “abc”, with the length of 3.
Example 2: Input: s = “bbbbb” Output: 1 Explanation: The answer is “b”, with the length of 1.
Example 3: Input: s = “pwwkew” Output: 3 Explanation: The answer is “wke”, with the length of 3. Notice that the answer must be a substring, “pwke” is a subsequence and not a substring.
Example 4: Input: s = “” Output: 0
Constraints: \(0 \le \text{s.length} \le 5 \times 10^4\) s consists of English letters, digits, symbols and spaces.
Solutions
We import some libraries that we will need later on.
import matplotlib.pyplot as plt
import numpy as np
import string
import random
import timeFor starters, we will write a function that generates random strings consisting of lowercase letters, digits, and whitespace characters of varying lengths. We will use it to see how our different solutions scale with increasing input size. When coding such problems, it’s essential to have abundant examples that cover all edge cases. By the way, I’ve found it easier to write and run my code in a Jupyter Notebook inside Visual Studio Code and then paste it to Leetcode.
def str_generator(size=6, chars=string.ascii_lowercase + string.digits + string.whitespace):
return ''.join(random.choice(chars) for _ in range(size))
# Print 10 random strings of random length [0,20)
input_str = [str_generator(size=random.randrange(0, 20)) for _ in range(10)]
print(input_str)
# ['75ypzflfi85wgbe', 'k4dogu\x0c14ckj', 'zcj8aoquhzfsh1g7uyh', '\x0cce\r\tt48nq1gio', 'c58',
# 'ol\tnfq7', 'i', 'jsjn\t8', '2tj\x0bb413', '']The horrible solution
My first attempt resulted in the following readable yet absolutely horrible, complexity-wise, solution. The rep() function is good, actually, and we will be using it in the other solutions as well. It uses a dictionary to track whether the next character has already been seen inside a substring. It has the advantage that it iterates only once the substring, so it’s \(\mathcal{O}(N)\) time complexity. Had we used a nested loop to search for repeating characters, that would lead us to \(\mathcal{O}(N^2)\) complexity from the get-go!
So, the following algorithm starts with the entire string and checks whether it has any repeating characters. If it doesn’t, then this is the longest substring of length N! Return its length, and we are done. If it has repeating characters, though, we slice it into two N-1 substrings. If the repeating characters are located in only one out of the two, we know that the other is the longest substring with a length N-1. Return it immediately, and we are done. Last, if there are repeating characters in both the substrings of length N-1, we need to dig deeper, and therefore we return the maximum length of the substring contained in these two substrings.
def rep(s:str) -> bool:
'''Returns True if str has repeating characters in it and False otherwise'''
freq = {}
for c in s:
if freq.get(c) != None:
return True
freq[c] = 1
return False
def helper(s:str, n:int) -> int:
'''The most horrible solution in terms of time and space complexity.
It uses recursion to generate the substrings, starting from the full
string and generating substrings.'''
if n < 2: return n
if not rep(s):
return n
a, b = s[:-1], s[1:]
rep_a, rep_b = rep(a), rep(b)
if not (rep_a and rep_b):
return n-1
else:
return max(helper(a, n-1), helper(b, n-1))
def verySlowLLS(s: str) -> int:
return helper(s, len(s))So, why does this algorithm perform so poorly? As I understand, there are two reasons: 1. Recursion is expensive because each time we call the helper() function, a new stack frame needs to be allocated, and 2. When we are calling max(helper(a, n-1), helper(b, n-1)), we don’t really divide the input, let alone conquer it! We merely go from N to N-1. It’s not as if we reduced the search space from N to N/2 or something. So, remember: if you recurse, you better be dividing the search space at each step, otherwise don’t recurse!
A decent solution of \(\mathcal{O}(N^2)\) complexity
The next two solutions use sliding windows, either forward or backward, to find all possible substrings in a string. The forward method keeps track of the length that is maximum at the current point in time. We need to do this because we must look up to the original string of length N.
def slowLLS_forward(s: str) -> int:
'''It uses sliding windows of length 1, 2, ..., N-1, N.
That's why we need to keep track of the currently maximum
length.'''
L = len(s)
if L < 2: return L
max_len = 0
for w in range(1, L+1):
for i in range(L - w + 1):
sub = s[i:(i+w)]
if not rep(sub):
current_len = len(sub)
if current_len > max_len:
max_len = current_len
return max_lenOn the other hand, if we are moving backward, i.e., if we are examining substrings of decreasing length, we know that the first substring without any repeating characters is the one with the maximum length.
def slowLLS_backward(s: str) -> int:
'''It uses sliding windows of length N, N-1, N-2, ..., 1.
That's why we don't need to keep track of the currently
maximum length. The first non-repeating substring we encounter
is the one with the maximum length.'''
L = len(s)
if L < 2: return L
for w in range(L, 0, -1):
for i in range(L - w + 1):
sub = s[i:(i+w)]
if not rep(sub):
return len(sub)The best solution of \(\mathcal{O}(N)\) complexity
This is actually the best solution I could come up with. We are using two variables to keep track of the start and the end of the currently maximum substring. Every time we see a non-repeating character, we advance the end of the presently maximal length substring. Contrastly, every time we encounter a repeating character, we advance the start of the currently maximal length substring. In this case, however, we need to remove from our dictionary all characters that we had discarded when we pushed the origin of the substring.
def fastLLS(s: str) -> int:
'''Calculate the longest non-repeating substring
on one go, by keeping track of the start (variable a) and
end (variable b) of the currently maximum such substring.'''
max_len = 0
a = 0
b = 0
track = {}
for i, c in enumerate(s):
if track.get(c, -1) == -1:
b = i
track[c] = i
else:
start = a
end = track[c] + 1
for j in s[start:end]:
del track[j]
a = end
b = i
track[c] = i
m = b - a + 1
if m > max_len: max_len = m
return max_lenIndeed, after submitting this solution to Leetcode I got:
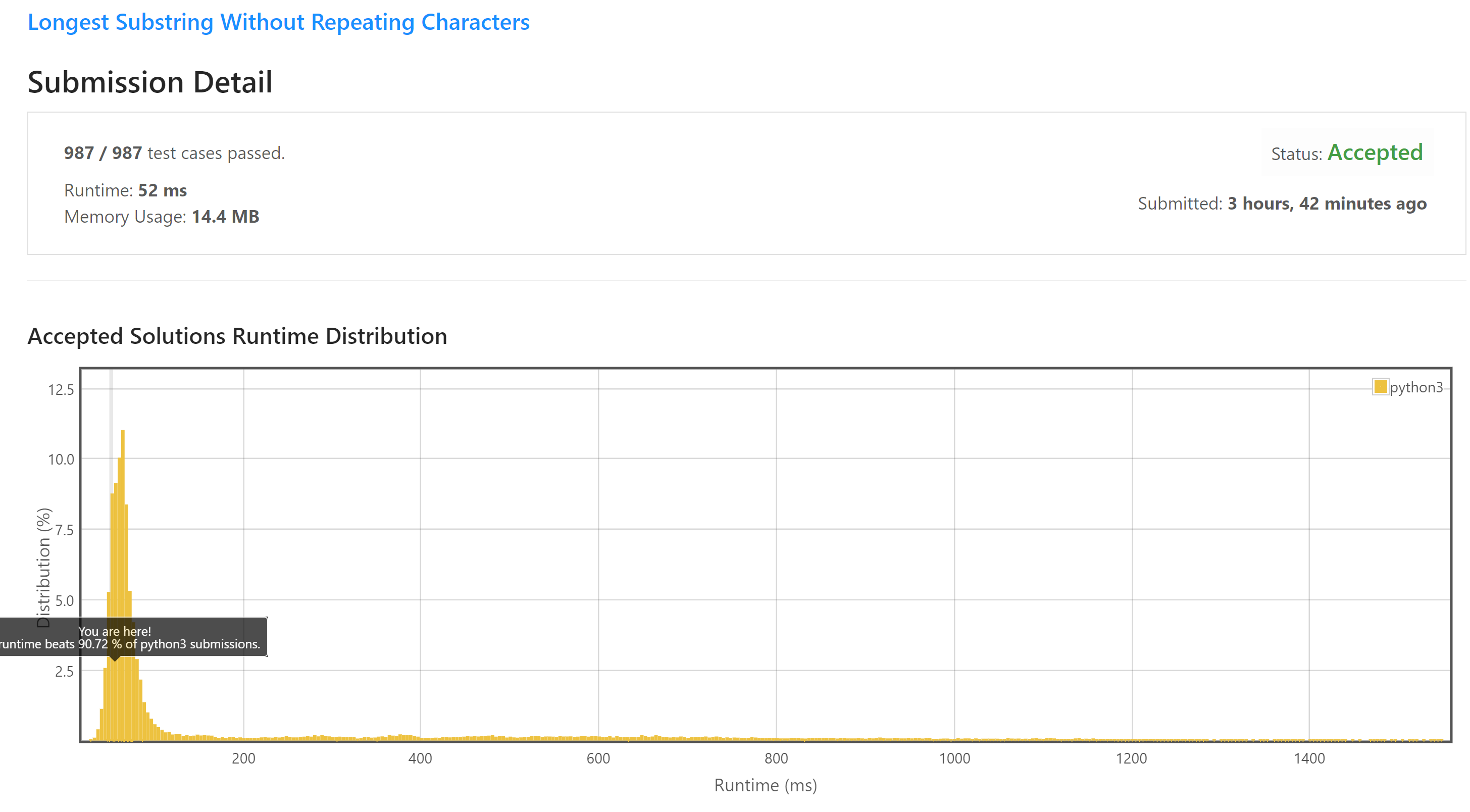
step = 2
def profile_function(f, n):
'''Profile `f' by applying it on input strings of
progressively increasing length up to `n'.'''
runtimes = []
for i in range(0, n, step):
input_str = str_generator(size=i)
start = time.perf_counter()
f(input_str)
runtimes.append([i, time.perf_counter() - start])
return runtimes
def plot_runtimes(r, fitDegree, title):
'''Plot runtimes along with a polynomial fit of `fitDegree' degree.
By default don't create figure / show the plot, so that we can call
this function inside a subplot() context.'''
#plt.figure()
plt.scatter(*zip(*r), s=5)
plt.xlabel('Input string length')
plt.ylabel('Execution time in sec')
plt.title(title)
# Add a polynomial fit
if fitDegree >= 0:
model = np.poly1d(np.polyfit(*zip(*r), fitDegree))
polyline = np.linspace(1, len(r) * step, 50)
plt.plot(polyline, model(polyline), 'r')
#plt.show()runtimes_very_slow = profile_function(verySlowLLS, 34)
plot_runtimes(runtimes_very_slow, -1, verySlowLLS.__name__)

runtimes_slow_forward = profile_function(slowLLS_forward, 1000)
plot_runtimes(runtimes_slow_forward, 2, slowLLS_forward.__name__)

runtimes_slow_backward = profile_function(slowLLS_backward, 1000)
plot_runtimes(runtimes_slow_backward, 2, slowLLS_backward.__name__)

runtimes_fast = profile_function(fastLLS, 10000)
plot_runtimes(runtimes_fast, 1, fastLLS.__name__)

As a sanity check, we verify that all algorithms return the same result for strings of various lengths. We can’t really go past a length of 30 characters because the recursive algorithm takes ages to run.
# Sanity check -- all algorithms should agree
for i in range(0, 30, 3):
input_str = str_generator(size=i)
y1 = fastLLS(input_str)
y2 = slowLLS_forward(input_str)
y3 = slowLLS_forward(input_str)
y4 = verySlowLLS(input_str)
if y1 != y2 or y2 != y3 or y3 != y4:
print(input_str)
print(y1, y2, y3, y4)
breakIn this plot we combine the running times of all algorithms side by side.
# Plot the runtimes of all algorithms side by side
plt.figure(figsize=(15,4))
plt.subplot(1,4,1)
plot_runtimes(runtimes_fast, 1, fastLLS.__name__)
plt.subplot(1,4,2)
plot_runtimes(runtimes_slow_backward, 2, slowLLS_backward.__name__)
plt.subplot(1,4,3)
plot_runtimes(runtimes_slow_forward, 2, slowLLS_forward.__name__)
plt.subplot(1,4,4)
plot_runtimes(runtimes_very_slow, 3, verySlowLLS.__name__)

plt.figure()
#plt.xscale('log')
plt.yscale('log')
plt.scatter(*zip(*runtimes_fast), s=5)
plt.scatter(*zip(*runtimes_slow_backward), s=10)
plt.scatter(*zip(*runtimes_slow_forward), s=10)
plt.scatter(*zip(*runtimes_very_slow), s=10)
plt.xlabel('Input string length')
plt.ylabel('Execution time in sec');
