Contents

Here, I’ll be adding questions regarding machine-learning and data-science in general. In the future, I’ll group them by subject.

What are collinearity and multicollinearity? How can we detect them?

Collinearity is the existence of two correlated predictor variables in a regression problem. Multicollinearity is when there are more than two variables correlated. Collinearity hurts regression, both coefficient estimation and the interpretation of the model. It can be detected with a scatterplot matrix, a correlation matrix, and via the calculation of Variance Inflation Factors (VIFs).

What’s a type I and type II error? Which one is worse?

Type I is a false positive (you tell a healthy man he has cancer). Type II is a false negative (you say to a man with cancer he is healthy). Regarding which one is worse, it depends on the context. A false negative for a spam filter isn’t a big deal, but a false negative for a cancer diagnostic test it is.

What is a ROC curve?

ROC stands for Receiver Operating Characteristic. ROC curve is a plot of True Positive rate (sensitivity) vs. False Positive rate (1-specificity) for different diagnostic test cut-off values. It demonstrates the inherent tradeoff of sensitivity vs. specificity (e.g., a covid test that is too sensitive won’t miss any real covid cases but will have a high number of false-positive). The close the curve on the left/upper-hand border of the plot, the better. A random classifier is represented by a 45-degree diagonal line. The area under the curve (AUC) is a measure of the test’s accuracy.

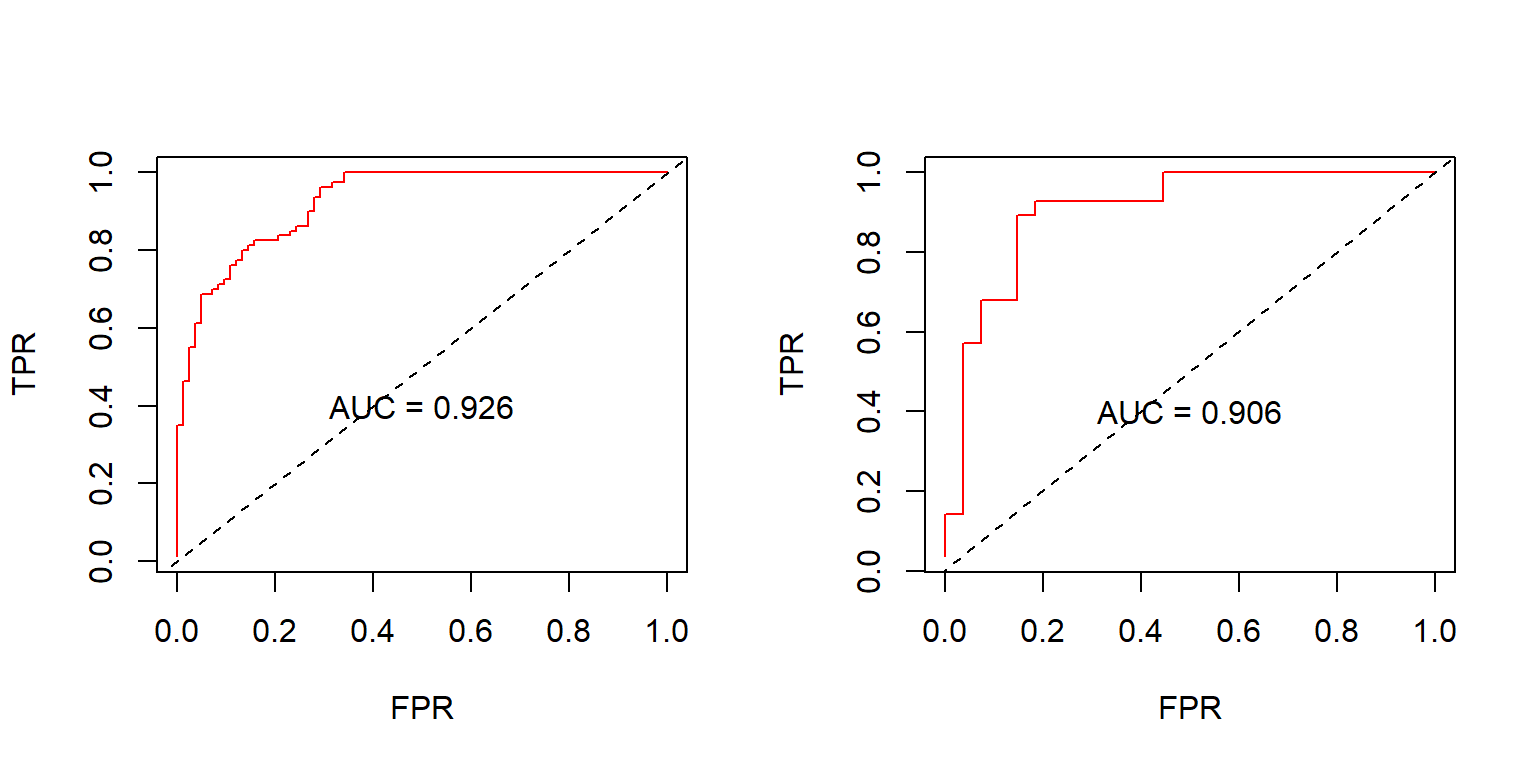
A ROC curve

What are the differences between K-nearest neighbor (KNN) and k-means clustering (K-Means)?

KNN is a supervised algorithm, K-Means is an unsupervised technique. The former is used for classification or regression, the latter for clustering. In KNN, “k” is the number of nearest neighbors used to perform the classification (or regression). In K-Means is the number of clusters the algorithm will come up with.

What is a confusion matrix?

It is a matrix used for evaluating a classification algorithm. The diagonal elements consist of true negative and true positive, whereas the off-diagonal consist of false negative and false positive.

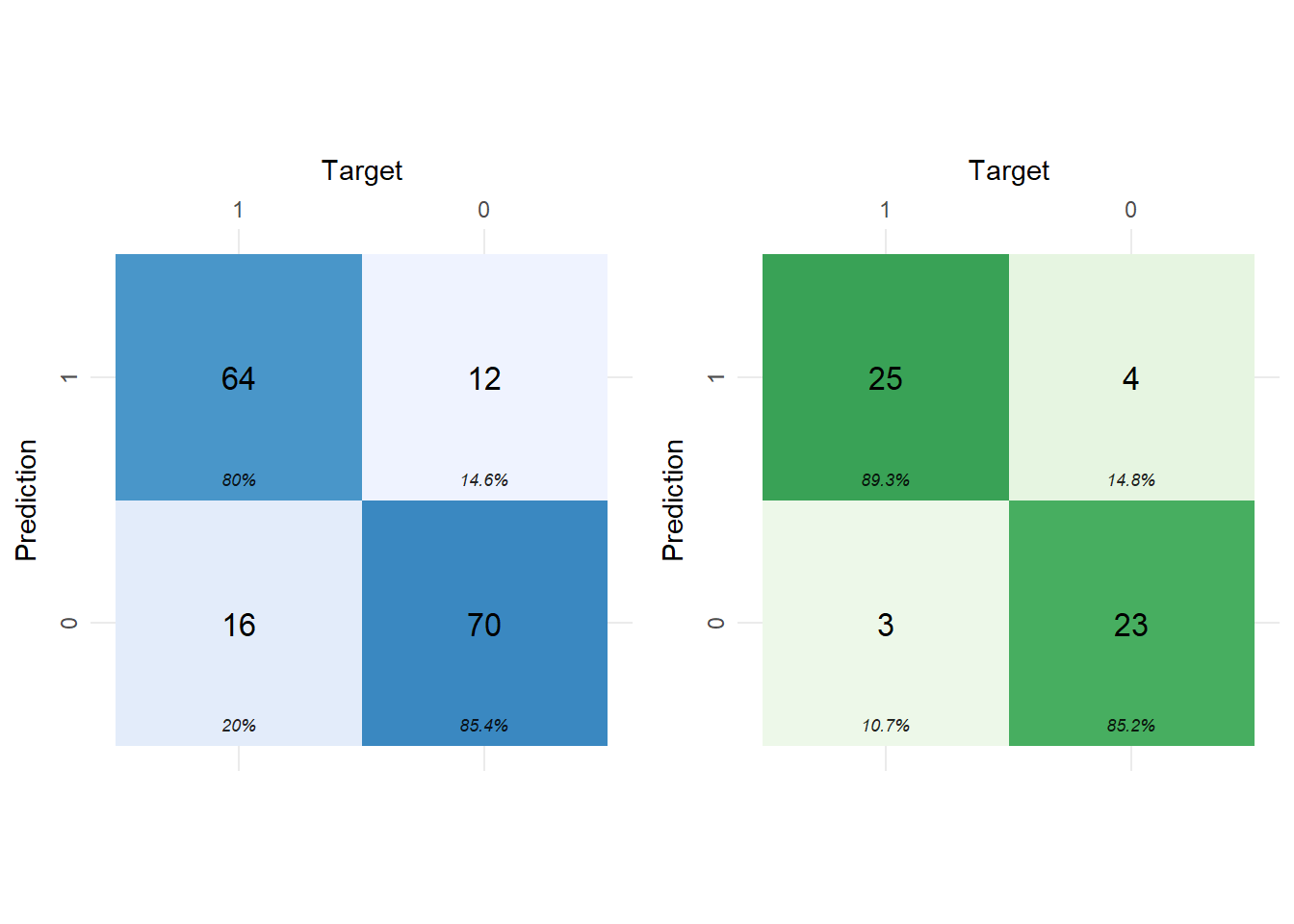
A confusion matrix

What are some differences between classification and regression?

In classification, the model predicts discrete class labels, in regression some continuous quantity. A classification problem with two classes (e.g., yes/no, spam/not spam, legit/fraud) is called binary and multi-class when there are more than two classes. A regression problem with many input variables is called a multivariate regression problem. Predicting the value of a cryptocoin over a period of time is a regression problem.

What is reinforcement learning?

It is when an agent interacts with its environment by generating actions and then discovers rewards or penalties. It is suited for problems that are reward-based.

What is bias, variance, and the bias-variance tradeoff?

Bias error is the difference between the average prediction of a model and the correct value we want to predict. A model with high bias is a model that doesn’t learn from the training data and is overly simplistic. The model will perform poorly to the training data and the test data.

Variance is the variability of a model’s prediction for a given data point. A high variance means that the model is learning from the training data more than there exists to learn. The model will perform very well on the training data but poor on the test data.

If we make our model too simple, we will decrease its variance but also increase its bias. If we make it too complex, we will reduce its bias but also increase its variance. This is the bias-variance tradeoff.

The model’s total error is the sum of the bias squared, the variance, and the irreducible error. The latter is a term that we can’t reduce no matter how good a model we build.

What is a lambda function, and when do we use one?

It’s a function without a name, i.e., an anonymous function. We use lambda functions when we need them for a short period of time, and then we dispose of them. For instance, to sort a list of tuples in Python based on the value of the second element, we would write:

lst_of_values = [('bob', 18), ('alice', 25), ('george', 99), ('stathis', 10)]
print(lst_of_values)
[('bob', 18), ('alice', 25), ('george', 99), ('stathis', 10)]

sorted_lst = sorted(lst_of_values, key=lambda x: x[1])
print(sorted_lst)
[('stathis', 10), ('bob', 18), ('alice', 25), ('george', 99)]

Lambda functions can have any number of parameters, but they can have only one statement.

What is the difference between a tuple and a list in Python?

Tuples are immutable, i.e., their contents cannot be mutated (changed) after their creation. Lists are mutable, i.e., their contents can be modified after their creation.

pl = ('alice', 'car', 54)
tpl[2] = 10    # Trying to modify the last element will throw an error

---------------------------------------------------------------------------
TypeError                                 Traceback (most recent call last)
<ipython-input-4-5bf6c4bd3643> in <module>
      1 tpl = ('alice', 'car', 54)
----> 2 tpl[2] = 10
TypeError: 'tuple' object does not support item assignment

What is broadcasting in Numpy?

Broadcasting in Numpy (and in Tensorflow) is the expansion of arrays so that their new shape would allow certain mathematical operations to take place. Example:

import numpy as np
# shape (4,1)
a = np.array([[1.],
              [2.],
              [3.],
              [4.]])
# shape (3,)
b = np.array([0., 1., 2.])

a + b

array([[1., 2., 3.],
       [2., 3., 4.],
       [3., 4., 5.],
       [4., 5., 6.]])

Here the array b is expanded from (3,) to (1,3) by replicating [0., 1. 2.] three times, and a is replicated 4 times along the second axis. The end result is:

[ [1., 1., 1.],    +  [ [0., 1., 2.],  
  [2., 2., 2.],         [0., 1., 2.],  
  [3., 3., 3.],         [0., 1., 2.],  
  [4., 4., 4.] ]        [0., 1., 2.] ]

The broadcasting rule is “Prepend 1s to the smaller shape, then check that the axes of both arrays have sizes that are equal or 1, and finally stretch the arrays in their size-1 axes.”. Broadcasting allows writing compact code but is also a source of confusion and errors.

What is the difference between classification and clustering?

Classification is supervised learning, where we assign a label class to some input. E.g., the input is a human face, and the label is whether the facial expression (neutral, smiles, sad, etc.). Clustering is unsupervised learning where we put similar inputs together without actually providing the labels. In a sense, the model will figure out the labels by itself. E.g., we provide a list of furniture images, and the model will put all the tables in a cluster in the feature space, all the chairs in another cluster in the feature space, etc.

What is regularization? What are the L1 and L2 regularization methods, and how do they differ?

Regularization is the process of controlling the model complexity (e.g., the number of model parameters or the values the parameters take). It is realized as an additional term that is added to the loss function. The number of the model’s parameters is regularized by L1 (also known as LASSO) and the weights by L2 (also known as ridge). In the following figure, the effects of L1 and L2 regularization are shown for increasing values of the regularization parameter. L1 invokes sparsity by driving some of the model’s parameters to become zero (this is some sort of feature selection). L2 makes all the model’s parameters small; however, it does not force them to become precisely zero.

LASSO vs ridge regularization

You can read more here

What is an eigenvector? And what is an eigenvalue?

The eigenvector is a vector whose direction remains unchanged after a linear transformation is applied to it. The eigenvalue is the scalar by which an eigenvector is scaled when a linear transformation is applied to it. For a square matrix \(A\), a vector \(\mathbf{x} \ne 0\), and some number \(\lambda\), it holds that \(\mathbf{A} \mathbf{x} = \lambda \mathbf{x}\). In the following example the eigenvector is \(\mathbf{x} = (-2, 1)\) and the eigenvalue \(\lambda = -2\).

\[\left( \begin{matrix} 1 & 6\\ 3 & 4 \end{matrix} \right) \cdot \left( \begin{matrix} -2\\1 \end{matrix} \right) = -2\cdot \left( \begin{matrix} -2\\ 1 \end{matrix} \right)\]

What is a token in the context of NLP, and how can we tokenize?

A token is a word in a sentence, and a sentence in a paragraph. NLTK is a Python library for doing natural language processing:

>>> import nltk
>>> import nltk.tokenize
>>> nltk.tokenize.sent_tokenize('NLTK is a Python library. It is used for natural language processing. It is used among other things for information retrieval in machine learning.')
['NLTK is a Python library.', 'It is used for natural language processing.', 'It is used among other things for information retrieval in machine learning.']
>>> nltk.tokenize.word_tokenize('Word tokenization happens at the word level, as opposed to sentence tokenization!')
['Word', 'tokenization', 'happens', 'at', 'the', 'word', 'level', ',', 'as', 'opposed', 'to', 'sentence', 'tokenization', '!']
>>>

What are unigrams, bigrams, trigrams, and n-grams?

Unigrams, bigrams, trigrams and n-grams is the parsing of text one, two, three, or n- words at a time:

>>> import nltk
>>> text = 'Parsing n- words at a time generates n-grams'
>>> list(nltk.ngrams(nltk.word_tokenize(text), 1))
[('Parsing',), ('n-',), ('words',), ('at',), ('a',), ('time',), ('generates',), ('n-grams',)]
>>>
>>> list(nltk.ngrams(nltk.word_tokenize(text), 2))
[('Parsing', 'n-'), ('n-', 'words'), ('words', 'at'), ('at', 'a'), ('a', 'time'), ('time', 'generates'), ('generates', 'n-grams')]
>>>
>>> list(nltk.ngrams(nltk.word_tokenize(text), 3))
[('Parsing', 'n-', 'words'), ('n-', 'words', 'at'), ('words', 'at', 'a'), ('at', 'a', 'time'), ('a', 'time', 'generates'), ('time', 'generates', 'n-grams')]
>>>

What is stemming in the context of NLP?

It is the process of removing and prefixes or suffixes to get the root of a word:

>>> from nltk.stem.porter import PorterStemmer
>>> stemmer = PorterStemmer()
>>> words_to_stem = ['interesting', 'candies', 'fireflies', 'eggs', 'implicated']
>>> [stemmer.stem(w) for w in words_to_stem]
['interest', 'candi', 'firefli', 'egg', 'implic']
>>>

What is the difference between Embedding vectors vs. One-hot vectors in the context of NLP?

One-hot vectors do not capture the level of similarity between words, since every one-hot vector has the same Euclidean distance from any other one-hot vector. Embedding vectors such as Word2Vec or GloVe vectors provide much more useful representation about the meaning of individual words.

Write a Python function that returns the index of the first duplicate element or -1 if none.

lst = [1, 0, 3, 5, -8, 100, -8, 20, 30, 40, 2, 31, 5]

# O(N^2) time complexity, O(1) space complexity
def find_dup(target_list):
    L = len(target_list)
    for i in range(L-1):
        for j in range(i+1, L):
            if target_list[i] == target_list[j]:
                return i

    return -1

# Homework: Write a similar function with
# O(N) time complexity and O(N) space complexity
def find_dup2(target_list):
    pass

# Should return the same
print(find_dup(lst))
print(find_dup2(lst))

What happens when a neural network’s weights are initialized near zero?

Assuming a sigmoid activation function, its Taylor expansion around zero is:

\[f(x) = \frac{1}{1 + \exp(-x)} = \frac{1}{2} + \frac{x}{4} - \frac{x^3}{48} + \mathrm{O}(x^5)\]

Therefore, for values of \(x\) near zero, the sigmoid function acts like a linear function:

\[f(x) \simeq \frac{1}{2} + \frac{x}{4}\]

As the network is trained, and the weights increase, non-linearities are introduced as needed.